étude d'une fonction définit par une racine - Exercice corrigé - 2 Bac Biof

étude de fonctions

problème

On considère la fonction $f$ définit sur $\mathbb{R}$ par: $$ f(x)=\sqrt{x^2+1}-x$$ et $\left( \mathcal{C}_f\right) $ sa courbe représentative dans un repère orthonormé.

1. monter que $\left( \forall x \in \mathbb{R} \right) $ , $f(x)>0$.
2. montrer que: $$\left( \forall x \in \mathbb{R} \right) \: f(x)+2x=\frac{1}{f(x)}$$
3. • a) évaluer la limite de $f$ en $-\infty$.
   • b) monter que la droite $(D)$ d'équation $y=-2x$ est une asymptote de $\left( \mathcal{C}_f\right) $ au voisinage de $-\infty$.
   • c) étudier les position relatives de $\left( \mathcal{C}_f\right) $ et la droite $(D)$.
4. • a) évaluer la limite de $f$ en $+\infty$.
   • b) en déduire que $\left( \mathcal{C}_f\right) $ admet une autre asymptote $(\Delta)$ au voisinage de $+\infty$.
5. monter que pour tout $x \in \mathbb{R}$ on a:$$ f'(x)=-\frac{f(x)}{\sqrt{x^2+1}}$$
6. poser la table de variations de la fonction $f$.
7. déterminer l'équation de la tangente $(T)$ à $\left( \mathcal{C}_f\right) $ au point d'abscisse $0$.
8. étudier la position de $\left( \mathcal{C}_f\right) $ par rapport à $T$.
9. construire la courbe $\left( \mathcal{C}_f\right) $.

correction

la fonction $f$ est définit sur $\mathbb{R}$ avec $ f(x)=\sqrt{x^2+1}-x$.

1. montrons que $f(x)$ est toujours positive. on a deux cas à distinguer :
   1. [cas où $x \leq 0$ :] dans ce cas on a $ \sqrt{x^2+1} > 0$ et comme $x \leq 0$ alors $ -x \geq 0$ donc $$\sqrt{x^2+1} -x >0$$ d'où $f(x)$ est strictement positive pour $x \leq 0$.
   2. [cas où $x \geq 0$ :] dans ce cas on a : $x^2+1 > x^2$ par suite $\sqrt{x^2+1} > \sqrt{x^2}$ comme $ x \geq 0$ on a $\sqrt{x^2}=x$. $$\sqrt{x^2+1} > x$$ d'où $\sqrt{x^2+1} - x >0$ $\\$ d'où $f(x)$ est strictement positive pour $x \leq 0$. finalement et par le principe de disjonction des cas on conclut que $\left( \forall x \in \mathbb{R} \right) $ , $f(x)>0$.
2. montrons que: $\left( \forall x \in \mathbb{R} \right) \: f(x)+2x=\frac{1}{f(x)}$. on a : \[ \left. \begin{array}{c c c} f(x)+2x & = & \sqrt{x^2+1}-x+2x \\ \\ & = & \sqrt{x^2+1}+x \\ \\ & = & \frac{\left( \sqrt{x^2+1}+x \right) \left( \sqrt{x^2+1}-x\right) }{\sqrt{x^2+1}-x} \\ \\ & = & \frac{ \sqrt{x^2+1} ^2 -x^2 }{\sqrt{x^2+1}-x} \\ \\ & = & \frac{ x^2+1 -x^2 }{\sqrt{x^2+1}-x} \\ \\ & = & \frac{1}{\sqrt{x^2+1}-x} \\ \\ & = & \frac{1}{f(x)} \end{array} \right. \] où dans la troisième ligne on a multiplié par le conjugué de $ \sqrt{x^2+1}+x $.
3. • a) calculons la limite de $f$ en $-\infty$. on a : $$\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \sqrt{x^2+1}-x=+\infty $$ car $\lim_{x \to -\infty} \sqrt{x^2+1}=+\infty $ et $\lim_{x \to -\infty} -x=+\infty$.
   • b) montons que la droite $(D)$ d'équation $y=-2x$ est une asymptote de $\left( \mathcal{C}_f\right) $ au voisinage de $-\infty$. pour cella on montre que: $$\lim_{x \to -\infty} f(x)-(-2x)=0$$ on a $$\lim_{x \to -\infty} f(x)-(-2x)=\lim_{x \to -\infty} f(x)+2x = \lim_{x \to -\infty} \frac{1}{f(x)} $$ or $\lim_{x \to -\infty} f(x)=+\infty$ donc $\lim_{x \to -\infty} \frac{1}{f(x)}=0$ $\\$ finalement $\lim_{x \to -\infty} f(x)-(-2x)=0$ $\\$ d'où la conclusion.
   • c) on a $f(x)-(-2x)=f(x)+2x=\frac{1}{f(x)}$ et comme $f$ est toujours strictement positive on déduit que $f(x)-(-2x) > 0$ donc $f(x)>-2x $, on conclut que $\left( \mathcal{C}_f\right) $ est toujours au dessus de $(D)$.
4. • a) calculons la limite de $f$ en $+\infty$. on a : $$\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \sqrt{x^2+1}-x $$ par multiplication par le conjugué on aura : $$\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{1}{\sqrt{x^2+1}+x}=+\infty $$ car $\lim_{x \to +\infty} \sqrt{x^2+1}=+\infty $ et $\lim_{x \to +\infty} x=+\infty$. $\\$ en déduit que : $$\lim_{x \to +\infty} f(x) =0 $$
   • b) d'après la question précédente on a $\lim_{x \to +\infty} f(x) =0 $ , en déduit que $\left( \mathcal{C}_f\right) $ admet la droite $(\Delta)$ d'équation $y=0$ comme asymptote horizontale au voisinage de $+\infty$.
5. soit $x \in \mathbb{R}$ on a: \[ \left. \begin{array}{c l l} f'(x) & = & \left( \sqrt{x^2+1}-x \right)' \\ \\ & = & \left( \sqrt{x^2+1}\right) '-\left( x \right)' \\ \\ & = & \frac{(x^2+1)'}{2\sqrt{x^2+1}}-1 \\ \\ & = & \frac{2x}{2\sqrt{x^2+1}}-1 \\ \\ & = & \frac{x}{\sqrt{x^2+1}}-1 \\ \\ & = & \frac{x}{\sqrt{x^2+1}}-\frac{\sqrt{x^2+1}}{\sqrt{x^2+1}} \\ \\ & = & \frac{x-\sqrt{x^2+1}}{\sqrt{x^2+1}} \\ \\ & = & -\frac{\sqrt{x^2+1}-x}{\sqrt{x^2+1}} \\ \\ alors \: f'(x) & = & -\frac{f(x)}{\sqrt{x^2+1}} \end{array} \right. \]
6. on a $f'(x)= -\frac{f(x)}{\sqrt{x^2+1}}$ et pour tout $x \in \mathbb{R}$ $f(x) > 0$ et $\sqrt{x^2+1} > 0$ donc : $$ \forall x \in \mathbb{R} \: ; \: f'(x) < 0 $$ on déduit que la fonction $f$ est strictement décroissante. $\\$

   

   le tableau de variations de $f$

7. soit $(T)$ la tangente de $\left( \mathcal{C}_f \right) $ en $x=0$, l'équation de $(T)$ est : $$y=f'(0)(x-0)+f(0)$$ avec $f(0)=\sqrt{0^2+1}-0=1$ et $f'(0)=-\frac{f(0)}{\sqrt{0^2+1}}=-1$ $\\$ finalement $ (T):y=-x+1$.
8. pour la position de $\left( \mathcal{C}_f \right) $ et $(T)$ , on a: $$ f(x)-(-x+1)=\sqrt{x^2+1}-x+x-1\sqrt{x^2+1}-1$$ or $\sqrt{x^2+1} > 1$ pour tout $x \in \mathbb{R}$ on déduit que $ f(x)>(-x+1)$ pour tout $x \in \mathbb{R}$ $\\$ par conséquence $\left( \mathcal{C}_f \right) $ est au dessus de $(T)$.
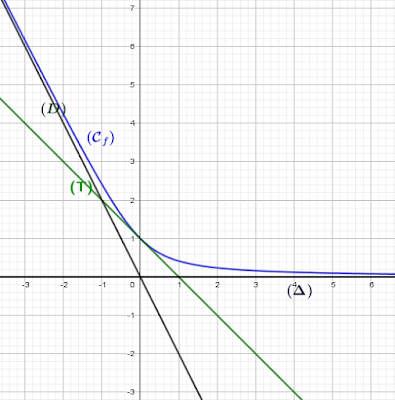
9. la courbe de $f$ est la suivante:

   

   la courbe de $f$