Généralités sur les suites numériques ... résumé du cour

Généralité sur les suites numériques

activite

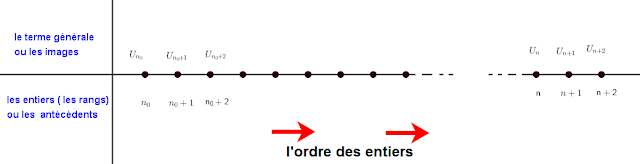
on considère une partie de $\mathbb{N}$ de forme $I_{n_0}=\lbrace n_0;n_0+1;n_0+2;....\rbrace$, par exemple $I_{3}=\lbrace 3;4;5;....\rbrace$ , $I_{10}=\lbrace 10;11;12;....\rbrace$ et $I_{0}=\lbrace 0;1;2;....\rbrace=\mathbb{N}$ $\\$ on considère la fonction $U$ définit par : $$ \left. \begin{array}{r c l} U: I_{n_0} &\mapsto& \mathbb{R} \\ n &\mapsto& U(n) \end{array} \right. $$ la fonction $U$ est définie sur une partie de $\mathbb{N}$ qui est $I_{n_0}$ contrairement à fonction numérique qui est définie sur une partie de $\mathbb{R}$$\\$ $U$ est dite une suite numérique , de plus l'image de $n$ est noté $U_n$ et non $U(n)$.

exemple

on a les suites suivantes: $$ \left. \begin{array}{r c l} U: I_{2} &\mapsto& \mathbb{R} \\ n &\mapsto& U_n=\frac{n}{n(n-1)} \end{array} \right. \left. \begin{array}{r c l} U: I_{10} &\mapsto& \mathbb{R} \\ n &\mapsto& U_n=\sqrt{n-10} \end{array} \right. $$ pour expliciter l'ensemble de définition de la suite on la note: $\left( U_n\right) _{n\geq n_0}$ ,$\left( V_n\right) _{n\geq n_0}$, $\left( W_n\right) _{n\geq n_0}$...

exemple

on utilise les notations suivantes pour exprimer les suites: $\\$ $\left( n^2+n-2\right) _{n\geq 0}$,$\left( \frac{1}{n}+1\right) _{n\geq 1}$,$\left( \sqrt{n-4}+n+1\right) _{n\geq 4}$. $\\$ on a la terminologie suivante:

1. la suite est noté $\left( U_n\right) _{n\geq n_0}$.
2. les images sont notés $U_n$, $U_n$ est dit le terme générale de la suite $\left( U_n\right) _{n\geq n_0}$.
3. $ U_{ n_0}$ est dit le premier terme.

la figure suivantes permet de schématiser la notions de suites numériques:

une suite numérique

définition

On appelle suite récurrente toute suite numérique dont le calcule d'un terme dépend d'un ou plusieurs terme le précédant. $\\$ par exemple la suite définit par : $$U_0=1 \:;\: U_{n+1}=U_n+2$$ dans ce cas on a : $U_0=1$ et $U_1=U_0+2=1+2=3$ et $U_2=U_1+2=3+2=5$. $\\$ un autre exemple est la suite de Fibonacci: $$U_0=1 \:;\: U_1=1\:;\: U_{n+2}=U_{n+1}+U_n$$ chaque terme $U_n$ ( pour $n \geq 2$ ) est la somme des deux termes qui le précédent. $\\$ on a : $\\$ $U_0=1$, $U_1=1$, $U_2=U_1+U_0=1+1=2$ et $U_3=U_2+U_1=2+1=3$ et $U_4=U_3+U_2=3+2=5$ $\\$ comme ça: la suite de Fibonacci suit le développement suivant : $$1;1;2;3;5;8;13;21;34;...$$

Suite majorée - minorée - bornée

définition

Soit $\left( U_n\right)_{n\geq n_0}$ une suite numérique.

1. on dit que $\left( U_n\right)_{n\geq n_0}$ est majorée s'il existe un nombre réel $M$ tel que : $$ \left( \forall n \geq n_0 \right) \: U_n \leq M$$
2. on dit que $\left( U_n\right)_{n\geq n_0}$ est minorée s'il existe un nombre réel $m$ tel que : $$ \left( \forall n \geq n_0 \right) \: m \leq U_n $$
3. on dit que $\left( U_n\right)_{n\geq n_0}$ est borné s'il est majorée et minorée c'est à dire s'il existe deux nombres réels $M$ et $m$ tels que : $$ \left( \forall n \geq n_0 \right) \: m \leq U_n \leq M$$

exemple

la suite $\left( u_n\right)_{n\geq 1}$ définit par $u_n=\frac{1}{n}$ est majorée par $M=1$ et est minorée par $m=0$, donc elle est bornée. $\\$ la suite $\left( v_n\right)_{n\geq 0}$ définit par $v_n=(-1)^n$ est majorée par $M=1$ et est minorée par $m=-1$, donc elle est bornée.

Suite croissante - décroissante - constante

définition

Soit $\left( U_n\right)_{n\geq n_0}$ une suite numérique.

1. on dit que $\left( U_n\right)_{n\geq n_0}$ est croissante si : $$ \left( \forall n \geq n_0 \right) \: U_n \leq U_{n+1}$$
2. on dit que $\left( U_n\right)_{n\geq n_0}$ est décroissante si : $$ \left( \forall n\geq n_0 \right) \: U_{n+1} \leq U_n $$
3. on dit que $\left( U_n\right)_{n\geq n_0}$ est constante si : $$ \left( \forall n \geq n_0 \right) \: U_{n+1} = U_n $$

remarque

Soit $\left( U_n\right)_{n\geq n_0}$ une suite numérique.

1. la suite $\left( U_n\right)_{n\geq n_0}$ est croissante si : $$ \left( \forall n \geq n_0 \right) \: U_{n+1}-U_n \geq 0$$
2. la suite $\left( U_n\right)_{n\geq n_0}$ est décroissante si : $$ \left( \forall n\geq n_0 \right) \: U_{n+1}-U_n \leq 0 $$
3. la suite $\left( U_n\right)_{n\geq n_0}$ est constante si : $$ \left( \forall n \geq n_0 \right) \: U_{n+1} - U_n=0 $$

exemple

la suite définie par $u_n=n^2+n$ est croissante . $\\$ en effet pour $n \in \mathbb{N}$ on a: $\\$ $u_{n+1}-u_n=(n+1)^2+(n+1)-(n^2+n)$ donc $u_{n+1}-u_n= n^2+2n+1+n+1-n^2-n$ donc $u_{n+1}-u_n= 2n+2$ or $2n+2 > 0$ donc la suite $(u_n)_{n \in \mathbb{N}}$ est croissante.

exemple

la suite définie par $v_n=\frac{1}{2n}-n+1$ est décroissante . $\\$ en effet pour $n \in \mathbb{N}^*$ on a: $\\$ $n < n+1$ donc $-n>-(n+1)$ et $\frac{1}{2n}>\frac{1}{2(n+1)}$ par addition membre par membre on a : $$ \frac{1}{2n}-n+1 > \frac{1}{2(n+1)}-(n+1)+1 $$ d'où $v_n>v_{n+1}$ pour $ \left( \forall n \in \mathbb{N}^* \right) $ $\\$ finalement la suite $(v_n)_{n \in \mathbb{N}^*}$ est décroissante. \end{exemple}

Suite arithmétique

définition

On dit qu'une suite $\left( U_n\right)_{n\geq n_0}$ est arithmétique s'il existe un nombre réel $r$ tel que : $$ \left( \forall n \geq n_0 \right) : U_{n+1}=U_n+r$$ le nombre $r$ est dit raison de la suite arithmétique $\left( U_n\right)_{n\geq n_0}$. \end{definition} la figure suivante illustre cette définition.

 suite arithmétique

Les séquences suivantes sont des suites arithmétiques : $$ 0;4;8;14;16;20;24;28;...$$ dans ce cas le raison est $r=4$. $$ 0;10;20;30;40;50;60;...$$ dans ce cas le raison est $r=10$. $$ -5;10;25;40;55;70;...$$ dans ce cas le raison est $r=15$.

remarque

pour monter qu'une suite $\left( U_n\right)_{n\geq n_0}$ est arithmétique on teste si la différence $U_{n+1}-U_n$ dépend de $n$ ou non. $\\$ si oui alors $\left( U_n\right)_{n\geq n_0}$ n'est pas arithmétique si non elle est.

exemple

soit $u_n=3n+1$ alors la suite $(u_n)_{n \in \mathbb{N}}$ est arithmétique de raison $r=3$ , en effet: $\\$ pour $ n \in \mathbb{N}$ on a $ u_{n+1}=3(n+1)+1=3n+3+1$ donc $ u_{n+1}=3(n+1)+1=3n+1+3=u_n+3$

proposition

soit $\left( U_n\right)_{n\geq n_0}$ une suite arithmétique, alors:

1. $ \left( \forall n \geq n_0 \right): U_{n+1}-U_n=r $
2. $ \left( \forall n \geq n_0 \right): U_n=U_{n_0}+(n-n_0)r $
3. $ \left( \forall n \geq n_0 \right):\left( \forall p \geq n_0 \right): U_n=U_p+(n-p)r $
4. Si $S$ désigne la somme $S=U_p+U_{p+1}+\cdots+U_n$ alors : $$ S=(n-p+1)\frac{U_p+U_n}{2} $$

Suite géométrique

definition

On dit qu'une suite $\left( U_n\right)_{n\geq n_0}$ est géométrique s'il existe un nombre réel $q$ tel que : $$ \left( \forall n \geq n_0 \right) : U_{n+1}=q.U_n$$ le nombre $q$ est dit raison de la suite arithmétique $\left( U_n\right)_{n\geq n_0}$. la figure suivante illustre cette définition.

suite_géométrique

Les séquences suivantes sont des suites géométriques : $$ 2;4;8;16;32;64;128;...$$ dans ce cas le raison est $q=2$. $$ 1;10;100;1000;10000;100000;...$$ dans ce cas le raison est $q=10$. $$ -5;10;-20;40;-80;160;...$$ dans ce cas le raison est $q=-2$.

proposition

soit $\left( U_n\right)_{n\geq n_0}$ une suite géométrique, alors:

1. $ \left( \forall n \geq n_0 \right): U_{n+1} \pm U_n=q $
2. $ \left( \forall n \geq n_0 \right): U_n=q^{n-n_0}U_{n_0} $
3. $ \left( \forall n \geq n_0 \right):\left( \forall p \geq n_0 \right): U_n=q^{n-p}U_p $
4. Si $S$ désigne la somme $S=U_p+U_{p+1}+\cdots+U_n$ alors : $$ S=\frac{1-q^{n-p+1}}{1-q} U_p$$