Les fonctions primitives ... résumé du cours

Les fonctions primitives

Notion de fonction primitive

définition

Soient $f$ et $F$ deux fonctions définit sur un intervalle $I$ telles que $F$ est dérivable sur $I$ et : $$\mathrm{\forall }x\in I:F^{\prime }(x)=f(x)$$ on dit que :

• la fonction $f$ est la dérivée de $F$ sur $I$.
• la fonction $F$ est une primitive de $f$ sur $I$.

exemple

on a les exemples suivants:

1. la fonction $F(x)=x^2$ est une primitive de $f(x)=2x$ sur $\mathbb{R}$.
2. la fonction $F(x)=5x+1$ est une primitive de $f(x)=5$ sur $\mathbb{R}$.
3. la fonction $F(x)=x^3$ est une primitive de $f(x)=3x^2$ sur $\mathbb{R}$.
4. la fonction $F(x)=sin(x)$ est une primitive de $f(x)=cos(x)$ sur $\mathbb{R}$.
5. la fonction $F(x)=\sqrt{x}$ est une primitive de $f(x)=\frac{1}{2\sqrt{x}}$ sur ${\mathbb{R}}_{+}^{\ast }$.

remarque

Soit $C$ une constante réelle c'est à dire $C\in \mathbb{R}$ .$$ Si $F$ est une primitive de $f$ sur $I$ alors : $${(F(x)+C)}^{\prime }=F^{\prime }(x)+C^{\prime }=f(x)+0=f(x)$$ par conséquence la fonction $F+C$ est encore une primitive de $f$ sur $I$. On parle donc d'ensemble des primitives de la fonction $f$.

exemple

• la fonction $F(x)=sin(x)+55$ est une primitive de $f(x)=cos(x)$ sur $\mathbb{R}$.
• la fonction $F(x)=sin(x)-22$ est aussi une primitive de $f(x)=cos(x)$ sur $\mathbb{R}$.
• la fonction $F(x)=sin(x)+123$ est aussi une primitive de $f(x)=cos(x)$ sur $\mathbb{R}$.

définition

soit $F$ une fonction primitive de $f$ sur un intervalle $I$, l'ensemble: $$\{F+C/C\in \mathbb{R}\}$$ est dit "ensemble des primitives" de la fonction $f$ sur $I$.

theoreme

soit $f$ et $g$ deux fonction numérique de fonction primitives $F$ et $G$ respectivement (sur un même intervalle $I$), alors:

• $F+G$ est une primitive de $f+g$ sur $I$.
• $\alpha .F$ est une primitive de $\alpha .f$ sur $I$.

pour calculer les fonction primitives on dispose du tableau suivant: $$\text{Misplaced hline}$$

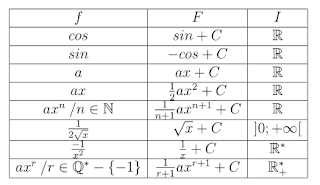les fonctions primitives tableau 1

 le théorème suivant indique dans quel cas on ait l'existence d'une fonction primitive.

théorème

si $f$ est une fonction continue sur un intervalle $I$ alors elle admet une primitive $F$ sur cette intervalle. Parmi les règles de calcul de primitive on a : $$\text{Misplaced hline}$$

les fonctions primitives tableau 2